Ein kombinatorische Problemstellung
Über Jahrhunderte hielt das 1637 formulierte Fermatsche Problem die Mathematikerwelt in Aufruhr, Generationen von mathematischen Genies und anderen geistigen Größen
bissen sich daran die Zähne aus, bis es schließ Anfang der 90er Jahre des 20. Jahrhunderts gelöst wurde. Ein Aufatmen ging durch die
Welt der Zahlentheoretiker und ewiger Ruhm ist Andrew Wiles und Richard Taylor gewiss: sie fanden den Beweis für die Gültigkeit
der Vermutung.
Eine Dimension kleiner, aber deswegen nicht minder aufregend präsentiert sich uns dieser Tage ein neues Problem; es handelt sich
dabei nicht um den Beweis einer zahlentheoretischen Vermutung, sondern um die Lösung eines praktischen, kombinatorischen Problems,
dem sich der ein oder andere Leser, bewusst oder unbewusst selbst schon gegenübersah: die Verteilung der Anzahl möglicher
Spielrunden im Spiel des Jahres 1984 Dampfross.
Zur Erläuterung:
In diesem Spiel gibt es eine Aufbauphase, in der alle 36 Städte, die sich auf dem Spielplan befinden, von den Spielern
mit Eisenbahnlinien erschlossen werden. Besitzt schließlich jede Stadt ihren eigenen Bahnhof, so startet die Betriebsphase:
in ihr werden zwischen den Mitspielern von Stadt zu Stadt Rennen auf den gebauten Eisenbahnlinien gefahren. Jede Stadt kann dabei
einmal als Start- und einmal als Zielpunkt fungieren. Anhand einer 6x6-Matrix, in der jedes Element für eine Stadt steht und
mit den Einträgen "0" für "war noch kein Startpunkt" und "1" für
"war bereits Startpunkt" kann der Spielverlauf für die Startbahnhöfe verfolgt werden. Das Gleiche gilt für die
Zielbahnhöfe. Das Spiel ist nach dem Rennen beendent, das dazu führt, dass sowohl in der Start- als auch der Zielmatrix
in jeder Zeile und in jeder Spalte mindestens einmal die 1 steht.
Die große Frage lautet: wie viele Rennen müssen durchschnittlich gefahren werden, bis das Spiel beendet ist? Oder auch einfach:
Wie ist die Anzahl der Rennen eines Spiels verteilt?
Nach 100000 simulierten Spielen reifte die Erkenntnis, dass der Erwartungswert der Verteilung bei 16 (arithmetisches Mittel=16.002) liegen muss. Dazu siehe auch das folgende Diagramm:
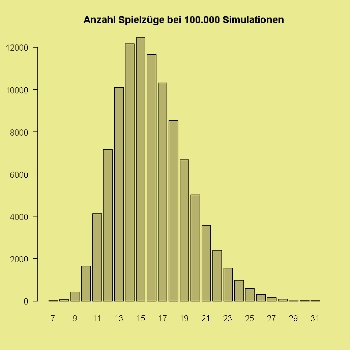
Die Herausforderung liegt also nicht direkt in der Verkündung des Erwartungswertes, sondern in der der
dahinterstehenden Dichtefunktion. Hiermit sei ein Wettbewerb ins Leben gerufen: Wer schafft es als erster, diese Funktion
herzuleiten? Als Belohnung winken Ruhm und Ehre, sowie die Aussicht auf statistische Unsterblichkeit. Man stelle sich hierzu
die typische Feststellung eines passionierten Dampfross-Spielers in nicht allzu ferner Zukunft zu Beginn der Betriebsphase vor: "Nach dem Erwartungswert
der Meier-Verteilung solten wir das Spiel nach 16 Runden beendet haben."
Lösungen und Lösungsversuche bitte an diese Adresse.